接触式三坐标测量透平叶片精度问题与解决方案
一直以来,接触式三坐标测量机以其通用性、高精度成为几何尺寸与形位公差测量的首选设备。到目前为止,还没有其它一种测量设备可以在几何测量领域具有如此广泛的应用。在透平叶片加工行业,接触式三坐标测量机也长久以来一直作为质量控制的检验手段,被广泛地应用于航空航天与发电设备透平叶片的型面与叶根尺寸与形位公差的检测。
不可否认,对于叶身型面普遍设定的80 ~ 200µm轮廓度公差,一般接触式三坐标测量机2µm左右的测量精度完全能够胜任测量工作。而对于精度要求较高的叶根装配尺寸,其5 ~ 10µm的公差也能采用精度1.5µm以上甚至是亚微米级高精度三坐标进行测量。叶片作为透平机械的关键部件之一,在检测方面有非常显著的特点与独特的要求。而三座标测量机作为一种通用测量设备,能否完全贴合透平叶片检测的特点一直是一个疏于探究的课题。或者说,从三坐标测量的原理上目前还没有找到一个完美的方案来解决叶片测量所遇到的问题。
图1 叶片测量特征截面型线
叶片型面测量一般以特征截面(控制截面)的轮廓偏差与位置度偏差来评定,这些特征截面以某一平面为基准,具有特定的截面高度。截面与叶身型面的交线形成一组闭合的平面三维曲线,这组闭合曲线即为叶身型线,也就是叶片型面测量的对象。虽然每一条型线都处于平面内,但由于型线上每一个测点的法线方向都在做三维变化,因此它们不能被当做二维曲线来处理。正是由于这个原因,才造成了叶片型线测量中的一个难点,即测针半径补偿误差(余弦误差)的引入。
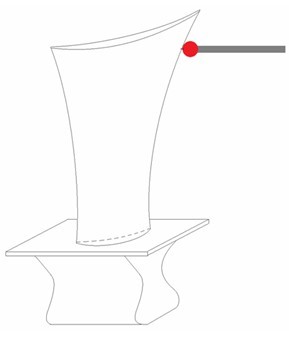
图2 接触式测量三维平面曲线
在测量叶片型线时采用的方法有两种,一种是将型线作为未知曲线来扫描,另一种则是将型线作为已知曲线来扫描,但这两种方法各有个的弊端。将叶片型线作为未知曲线扫描时,软件能够锁定扫描截面的高度,同时将测点矢量方向i,j,k的k分量设为0,以固定的Z值输出测点。当使用球形测针扫描型线时,红宝石球与三维曲面的实际接触点并不是预期的接触点(如图所示)。而测量软件记录的是红宝石球中心的空间坐标,然后根据测针半径来进行补偿,得出实际点的坐标。在这种情况下,测针尚未碰到预期接触点时已经触发,所以补偿后的接触点会存在半径补偿余弦误差。
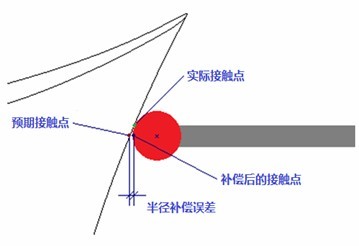
图3 余弦误差产生原因
为了量化这个余弦误差,我们分别以15°和30°倾角以及ø1和ø2测针来进行模拟计算,结果如下表所示:
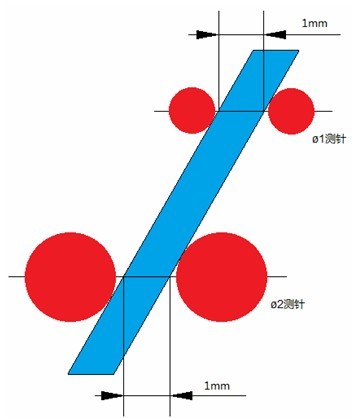
图4 不同直径测针的余弦误差比较
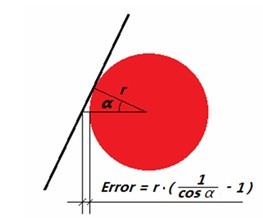
图5 余弦误差计算
|
叶身角度
|
测针直径
|
单边误差(mm)
|
双边误差(mm)
|
双边误差占叶片厚度百分比
|
|
15°倾角
|
Ø1测针
|
0.0176
|
0.0353
|
3.53%
|
|
Ø2测针
|
0.0353
|
0.0706
|
7.06%
|
|
30°倾角
|
Ø1测针
|
0.0774
|
0.1547
|
15.47%
|
|
Ø2测针
|
0.1547
|
0.3094
|
30.94%
|
表1 不同倾角与不同直径测针的余弦误差比较
我们可以发现,在使用相同测针情况下,当叶身的倾斜角度越大,所产生的余弦误差也越大;而在相同叶身倾角情况下,测针直径越大,余弦误差也越大。Ø1和Ø2测针是测量叶片最经常选用的测针规格,当叶身倾角达到30°时,产生的余弦误差甚至可以达到0.3mm之多,已经超出型线公差带的整体宽度,更是远远超出三坐标测量机本身的精度。
以上是将型线作为未知曲线来扫描的情况下会产生的问题。为了克服余弦误差带来的影响,另一种方法是将型线作为已知曲线,沿理论测点的矢量方向i,j,k来进行触发式采点。众所周知,没有任何一个零件可以做到100%与理论数据吻合,实际状态总会有一定的偏差存在。当测点矢量不是水平方向,且叶身型面存在偏差时,采到的实际点高度就会与理论高度Z产生偏差(如图所示)。
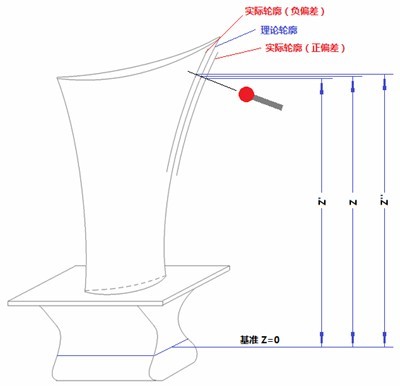
图6 法向采点时产生的截面测点高度差
我们同样以15°和30°倾角来进行模拟计算,当以法线方向进行采点时,测针直径不影响结果,因此不考虑测针直径,误差如下表所示:
|
叶身角度
|
型线偏差(mm)
|
测点高度误差(mm)
|
|
15°倾角
|
0.05
|
0.0125
|
|
0.1
|
0.025
|
|
30°倾角
|
0.05
|
0.0217
|
|
0.1
|
0.0433
|
表2不同倾角与不同型线偏差下的高度偏差比较
可以得出结论,这样测得的型线不是一条三维平面曲线,而是三维空间曲线。这样的型线无法对其一系列的叶型参数做出评价,除非软件对其进行投影等一些处理,将三维空间曲线转换成平面曲线,但是转换的过程势必会对实测曲线的精度造成影响。
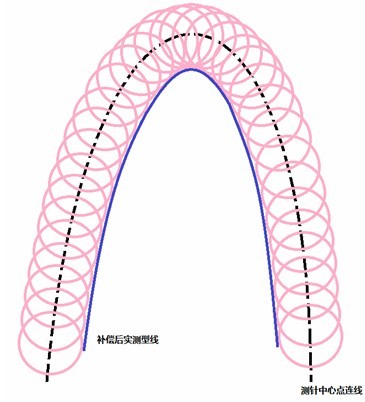
图7 采点与测针半径补偿
除了上述在叶片型线测量过程中出现的误差之外,在某些条件下还会出现型线形状失真的情况。这类情况出现的条件不尽相同,要究其原因的话就需要进行针对性的分析。如前所述,三坐标在采点过程中实际上记录的测针红宝石球中心的坐标值,然后根据测针半径做补偿,得到实际的测点,再进行几何元素构造(如图所示)。
有一种情况是当实际型线与理论型线位置偏差较大时,一部分测点的补偿方向会发生错误。原因在于,有些软件会根据距离最近的理论点来做出测针补偿,从而使用了`相反的矢量方向,造成了叶片型线边缘出现“钝头”的形状。
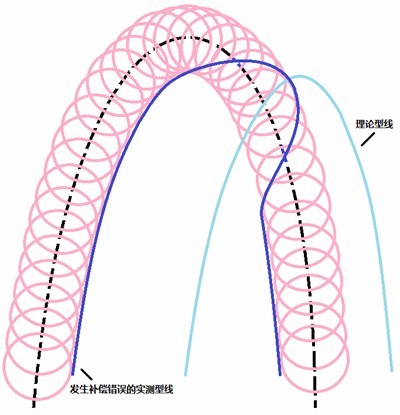
图8 因偏差过大引起的半径补偿方向错误
另一种情形是测点的序号不连续而发生跳跃,原本的测点顺序在某一个位置突然改变,造成测点序号不按曲线走向发展,而是来回变化,这样生成的型线会发生“打结”的现象。这种情况通常也是发生在型线偏差较大,测针在叶片边缘丢失较多测点的情况下。
图9 因丢点引起的测点序号不连续
综上所述,接触式三坐标测量机虽然本身精度较高,但是在测量透平叶片,尤其是型面倾斜扭转较大的航空叶片时,会产生较多问题。这些问题产生的原因与三坐标本身的精度关系并不大,而是从接触式测量的原理上就决定了它是无法避免的。那么针对这些问题,到底有没有解决方案来减轻甚至是规避这些影响呢?下面我们就两种方案来进行分析。
第一种方案我们还是从接触式三坐标测量机入手,探究如何规避余弦误差的方法。首先需要对叶片型面做一个增厚处理,沿着型面上每个点的法线方向增加所使用测针的球头半径厚度,得到新的叶片型面。形象地说,就是用一个直径为测针球头半径的小球在叶身上滚过,小球形成的外包络面即为新的型面(如图所示)。然后在测量型线时,关闭测量软件中的测针补偿功能,其效果相当于使用了球头直径为0的尖测针,以水平矢量方向来进行测量。这种方法在先期的理论型面增厚处理过程中,就已经考虑了余弦误差的存在,并消除了其带来的影响。
这个方法虽然解决了余弦误差带来的测量精度损失,但也并非是一个完美的解决方案。首先,叶片型面做了增厚处理后,新得到的型线已经不是原先的设计型线了。后续的测量以及得出的结果也是以处理后的型线为参考。虽然处理前后的理论型线有唯一的对应关系,并可以用增厚型线来反映设计型线的偏差情况,评价其轮廓度与位置度,但是所有的叶型参数评价都不再有意义。
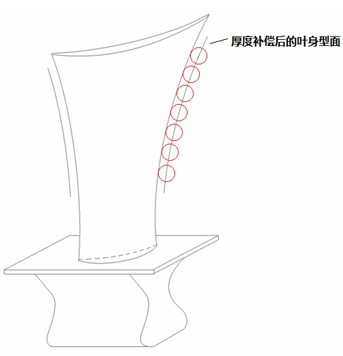
图10 零件材料厚度补偿
第二种方案我们跳出接触式三坐标测量机的范畴,诉诸于其它测量方法来解决这一问题。现今,光学测头正越来越多地应用到测量中,如果采用光学点测头来替代接触式测针,那从测量原理上就不存在半径补偿,那余弦误差和半径补偿方向错误等问题就可以迎刃而解。而且,以水平矢量方向进行测量得到的型线可以保证固定的测点高度,最终得出的也是基于理论设计的型线。
如果采用光学测头来测量透平叶片,又会引发一系列新的针对光学测头的考量,这些问题的深入探究不属于本文范围,在这里仅作一些启发式的介绍。首先,光学测头对于物体表面状态一般都有所要求,太过光亮或颜色过深的表面都会对反光造成负面影响。第二,由于叶片几何形状的特殊性,对于光学测头的工作距离要有一定的要求。某些种类的光学测头虽然可以达到较高的测量精度,但它的工作距离非常近,极易和叶片发生碰撞;如果通过换镜头来得到较大的工作距离,又会明显地降低测量精度。第三个需要关注的是表面入射角的范围,在测量零件过程中,如果一直以法线方向去采点,难免会碰到盲区,在这种情况下就需要改变入射光的矢量方向。如果光学测头的入射光允许角度范围较小的话,会给测量造成不便。最后也是非常重要的一点,光学测头的精度及验证方法,这个是整个测量过程及其结果可信度的基础。
总言之,接触式三坐标到目前为止一直是几何测量的首选手段,其应用也得到了长久的考验和广泛的认可。但是针对叶片测量等特殊应用进行深一步的探究,提高测量水平仍旧是一件有意义的工作。